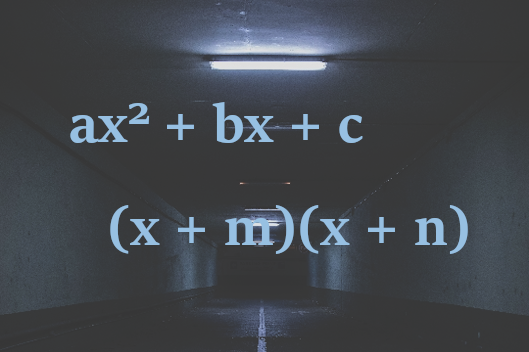
How do you factor an equation with a leading coefficient greater than 1?
Factoring an equation is a task that you will very commonly be asked to do on the SAT and ACT. You are basically converting a parabolic/quadratic equation/expression from the form ax2 + bx + c (where a is the leading coefficient, b is the x coefficient and c is the constant, or the term without an x or x2) into the form (x + m)(x + n), where m and n are numbers.
Factoring, in general, is not too difficult, once you know how to do it. For example, if we had an expression like this:
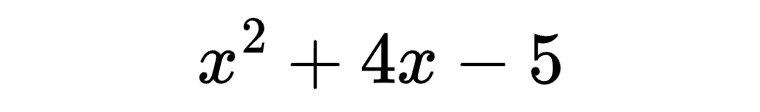
we would find two numbers whose product is c, the constant, or, in this case, -5, and whose sum is b, the coefficient of x, or 4. 5 and -1 would fit this criteria, so this is our m and n numbers. The factored form of this expression would be:
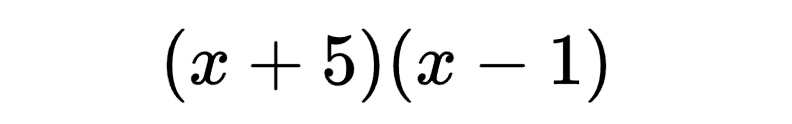
However, what would we do if the leading coefficient (the number in front of the x2 term) was not 1, but something else? Factoring something like 2x2 + 4x - 5 can't give us the same result as x2 + 4x - 5, after all.
Dealing with an expression that includes a leading coefficient greater than 1 involves a little more complexity than that typical, straightforward factoring method. So, to avoid some of the added complexity, the first thing you should always check is if you can eliminate that leading coefficient by dividing all the terms by the leading coefficient; if they all divide evenly, then you can apply this strategy.
For example, we might stumble across this expression:
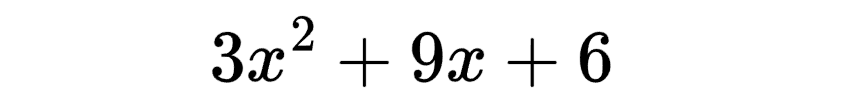
In this equation, we can divide all the terms by 3 and get 3(x2 + 3 + 2). We remove the leading coefficient, 3, from the main equation (it's still there, but outside the parentheses) so that we are left with an expression without a leading coefficient. Now, we can factor this expression like we normally would, finding two numbers that, when multiplied together, give us 2 and, when added together, given us 3. 2 and 1 work. So, we would end up with the expression 3(x + 2)(x + 1). That is certainly a valid factored form. But, we could also rewrite it as (3x + 6)(x + 1) if the problem requires it. Simply distribute (multiply) the 3 throughout the first term (or even the second term; it doesn't matter).
But, what if we can't evenly divide all the terms by the leading coefficient? What if we have an expression like this?
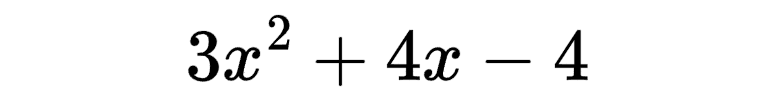
We can't simply divide all the terms by 3; we would get fractions that might be hard to work with. What we can do, though, is a variation of the basic factoring method we used earlier. Let's try to find two numbers that, when multiplied together, give us ac, the product of the leading coefficient, 3, and the constant, -4 (instead of just c), or -12, and, when added together, give us the coefficient of the x term, or 4. Thinking about all the factors of -12, the combination of factors that would work in this situation would be 6 and -2. 6 x -2 = -12 and 6 + -2 = 4.
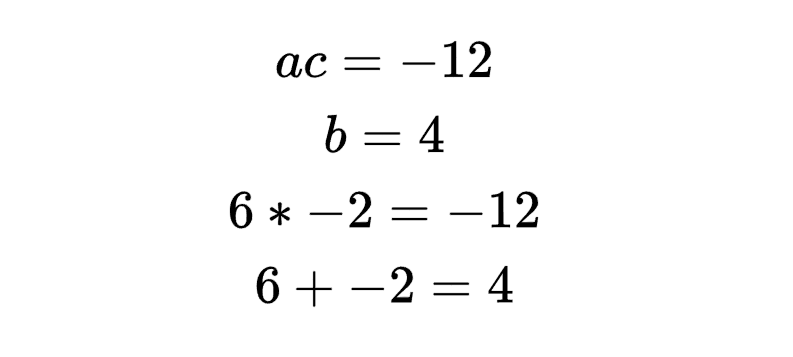
At this point, there are a lot of different ways to finish factoring, like pulling out the common factor, etc. But, I'm a very visual person and maybe even some of you are, too, so let's use my favorite method: the box method
What do we do with these two numbers, now? We will split the middle term, the x term, into two terms, giving us a four-term expression: 3x2 + 6x - 2x - 4. Why do that though? We want to draw a box (the box in the box method) consisting of four squares and fill them in with our four terms.
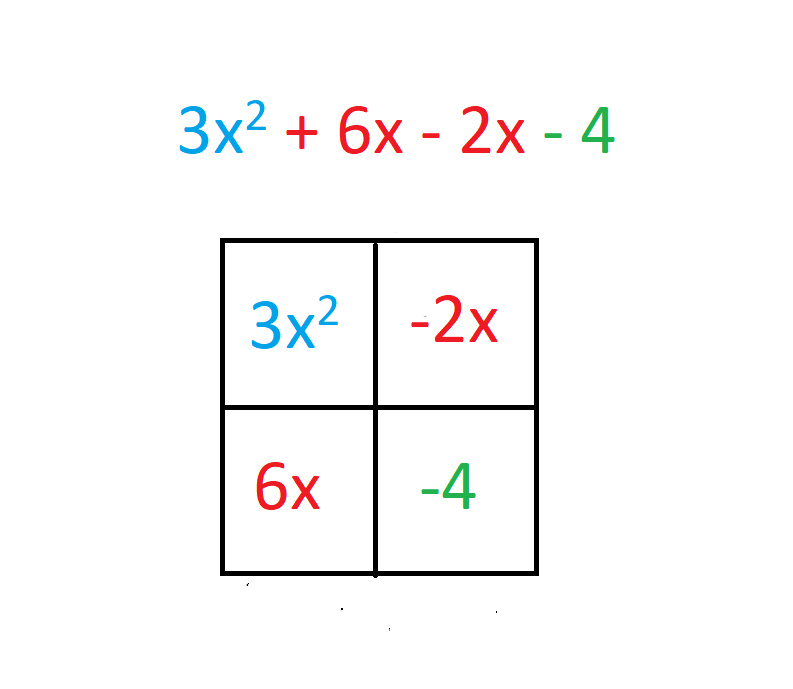
The first term, the x2 term (3x2), goes in the upper left-hand corner; the last term, the constant (-4), goes in the bottom right-hand corner. Then, we can put the two x terms (6x and -2x) into the last two squares; it doesn't matter which one goes where.
Then, we want to look at each column and each row and pull out the common factor of each term in that column or row. We will write that common factor outside the box, at the top of the column or at the beginning of the row.
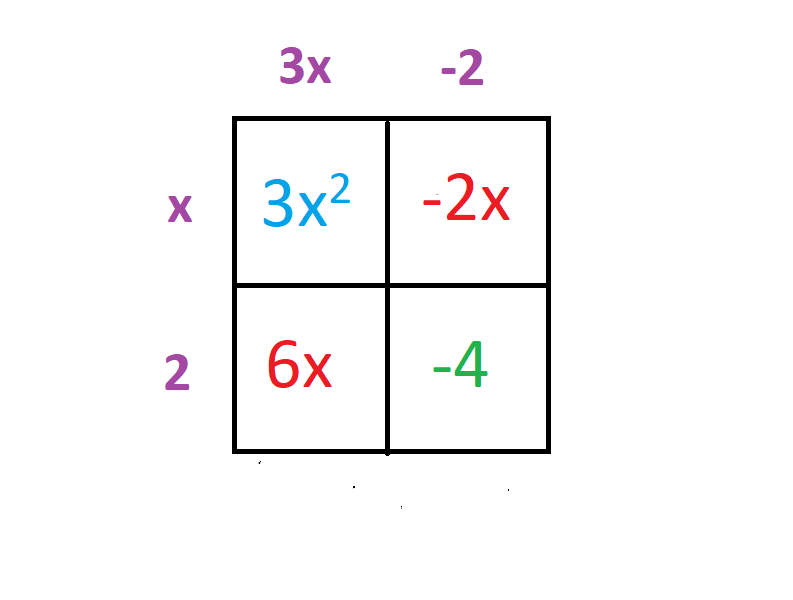
Starting with the first column, the common factor between 3x2 and 6x is 3x. We can divide both terms evenly by 3x. 3x2 divided by 3x is x and 6x divided by 3x is 2. So, we would write 3x at the top of that column and then move on to the next column.
The common factor between -2x and -4 is -2, so we would write that at the top of second column. Now, we move on to the rows. In the first row, the common factor between 3x2 and -2x is x. We would write that to the left of the first row. Finally, the common factor in the second row (between 6x and -4) is 2, so we would write that to the left of the second row.
The next step is to put all of this into a factored expression. To do that, we would take the common factors of the columns (3x and -2x) and combine them: (3x - 2). Then, we would take the common factors of the rows (x and 2) and combine those, as well: (x + 2).
We are left with a nice, factored expression: (3x - 2)(x + 2). This we could use to find the zeroes, simplify a large, complicated algebra problem... whatever we would need for the math problem we are working on.
That is how you can factor an expression that has a leading coefficient larger than 1. First, see if you can make it simpler and get rid of the leading coefficient by dividing all the terms by the leading coefficient. Then, if that doesn't work, you can use the box method to find the factored form.
