How do you determine the distance between any two points?

Sometimes you will come across an SAT or ACT Math problem that will ask you to find the distance between two points. For example, you may see something like this:

If you draw a line connecting these two points, you will see a perfectly vertical line:

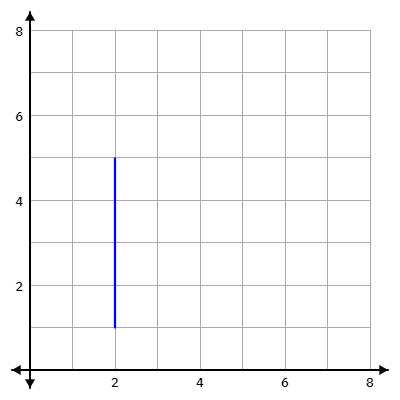
It would be easy to determine the distance between these two points. Just find the difference between the y values: 5 - 1 = 4. So, the distance between these two points is 4.

Now, let's shift the second coordinate point slightly to the right:

If we were to connect these two points, we would, again, have a line. However, this one is not perfectly vertical; it is at a slant:

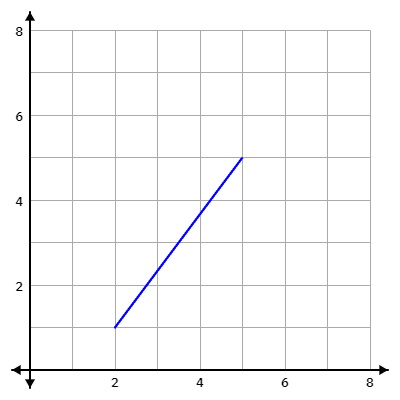
How would we find the distance between these two coordinate points? You can't simply find the difference between the y values (which would still be 4). The line above, if you look close, looks a little longer than the earlier vertical line.

Well, one simple way to find the distance between any two points is to use the distance formula:

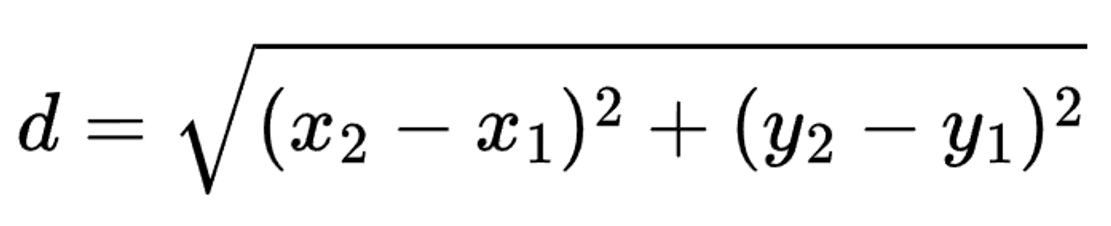
All we need to do now is fill in the coordinate points, then calculate the distance. The two xs are 2 and 5, and the two ys are 1 and 5.

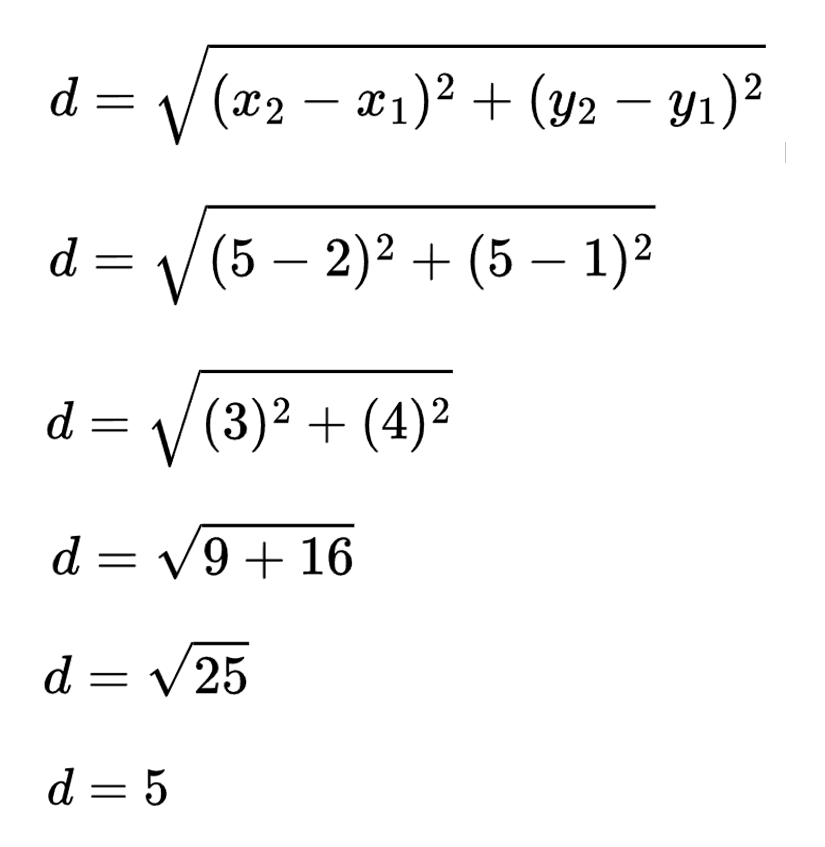
So, the distance between (2, 1) and (5, 5) is 5, slightly more than the distance between the original two points, (2, 1) and (2, 5).

But, let's say you didn't remember the distance formula (which is not hard to do; it's very complicated!). Neither the SAT nor the ACT will normally give you this formula at the beginning of the section or within the question itself. So, you will have to find another way.

Let's take a look at our two points again: (2, 1) and (5, 5). We could draw that line between them again, but, then, we could go a little further and create a right triangle, where this line containing the two coordinate points acts as the hypotenuse:

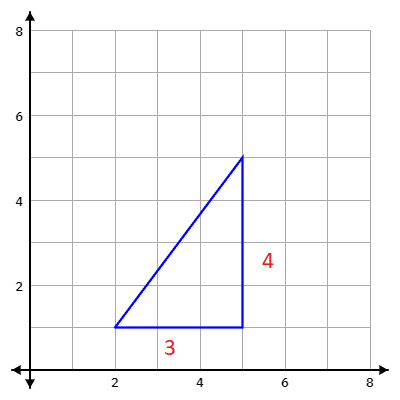
To find the distance between the two coordinate points, all we would have to do is find the hypotenuse of this triangle. We can use the pythagorean theorem to help use with that:

The two legs of the triangle are a and b, or, the difference in the xs and the difference in the ys. One leg of the triangle is a horizontal line that is the distance between the x coordinate points, which, in this triangle, is 3. The other leg of the triangle is a vertical line that is the difference in the y coordinate points, which, in this triangle, is 4.

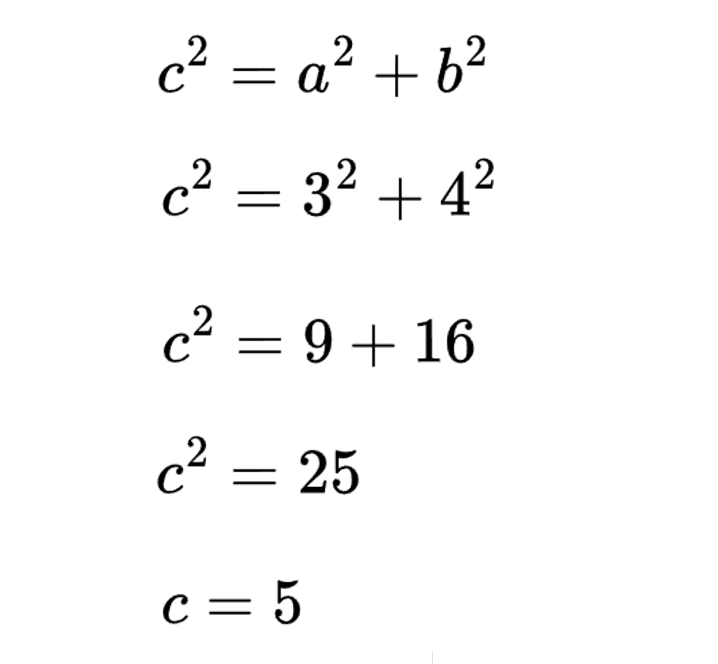
Drawing a triangle and using the pythagorean theorem gives us 5, just like we got by using the distance formula. And, if you look closely at the distance formula, it makes sense. The distance formula is really a variation of the pythagorean theorem. The legs, a and b, are represented by the difference in the xs (x2 - x1) and the difference in the ys (y2 - y1). Then, to find c, or the hypotenuse, or the distance, you would just take the square root of both sides.

So, now you have two ways to determine the distance between any two points. You can use the distance formula (if you remember it!) or you can simply ddraw a triangle and find the hypotenuse.